√100以上 立体の体積の求め方 公式 243818-立体の体積の求め方 公式

どちらも公式は簡単です。 柱の体積＝底面の面積×高さ 錐の体積＝底面の面積×高さ÷3 錐の高さは、頂点から底面に垂直に引いた線です。 真っ直ぐの線です。 斜めの線ではないので気をつけましょう。 （例題1） 上の図の円錐の体積は何cm²でしょう直方体の体積は『縦×横』の長方形が『高さ』分だけ積み上がったと考えると、体積は 『縦×横×高さ』 です。 立方体の場合、縦・横・高さがすべて一辺の長さとなるので、体積は 『1辺×1辺×1辺』 と表球の体積を求める公式は、V = 4/3 πr^3 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。 このページでは、例題と共に、この公式の使い方を説明しています。

角柱 円柱の表面積と体積の公式 数学fun

立体の体積の求め方 公式

立体の体積の求め方 公式- ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ！ めんどい計算式だけど、 円柱の表面積の求め方を3ステップで解説していくよ。 3ステップでわかる！円柱の表面積の求め方 例題をときながら円柱の表面積の求め方を勉強していこう。 例題 半径3cm、高さ10cmの円柱の表面積を求めなさい。 つぎの3ステップで求めることができるんだ。

球の表面積と体積の公式 数学fun

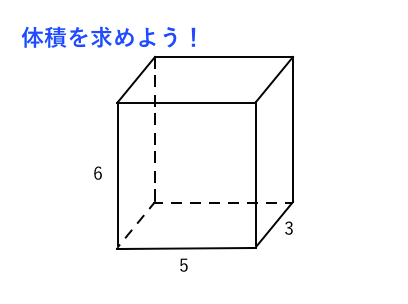
 立方体の体積の求め方公式 サイコロの形をしている立方体は、一辺の長さがどれも同じ。 立方体の体積は、次の公式で求められます。 立方体の体積＝1辺×1辺×1辺 直方体の体積の求め方公式 直方体の体積は、次の公式で求められます。体積の公式は、柱体（ちゅうたい）は「底面積×高さ」、錐体（すいたい）は「底面積×高さ×1/3」で計算できます。 この2つを暗記すれば、体積の公式は簡単です。 但し、三角柱と円柱では「底面積の計算式」が違うので注意しましょう。 今回は、体積の公式の求め方、覚え方と一覧、三角柱、円柱、三角錐の体積について説明します。 体積の意味など下記も参考Hello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。

 問題2）下の図2の長方形ABCDを、線分ABを回転の軸として1回転させてできる立体の体積は63 \(\pi\) ㎤だった。線分ABの長さを求めよ。 問1）30㎤ 問2）7cm 関連記事 中学数学「空間図形」② 位置関係・展開図・回転体のコツ 錐の体積 錐ってのは、柱から \( \frac{1}{3}\) だけ削り出してとんがらせた5年生で勉強した直方体や立方体の体積の求める公式を生かして、四角柱の体積の求め方を気づかせます。 5年で勉強した 立方体と直方体の体積 の求め方をふりかえります。 立方体の体積＝1辺×1辺×1辺 直方体の体積＝たて×横×高さ 5年で勉強した 角柱と円柱の立体の形をふりかえります。 角柱 角柱 角柱 円柱 立方体 直方体 三角柱 円柱 上の図から立方体と直方7立体の体積 と表面積 また，中心角は上の④の公式を用いると， 4 8 ×360°＝180° と求められる。 答 48∏cm2 142 次の図の円錐の体積を求めよ。 ⑴ ⑵ ⑶ ¬＝2∏r 115中学の数学幾何I_H_p0357indd 495中学の数学幾何I_H_p0357indd 49 626 PM6129 626 PM 2章 空間図形 50 144 次の図の円錐の表

 V = ∫ − r r π { r 2 − x 2 } 2 d x = 2 π ∫ 0 r ( r 2 − x 2) d x = 2 π r 2 x − x 3 3 0 r = 4 3 π r 3 V=\displaystyle\int_ {r}^r\pi\ {\sqrt {r^2x^2}\}^2dx\\ =2\pi\displaystyle\int_ {0}^r (r^2x^2)dx\\ =2\pi\left r^2x\dfrac {x^3} {3}\right_ {0}^r\\ =\dfrac {4} {3}\pi r^3 V = ∫ −rr（体積の計算） 立体の体積を求めるには，体積の微分が断面積になることを利用します． すなわち，左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し， x における断面積を S(x) とおきます． 上で復習した面積の求め方と同様にしてこの立体の体積は、元の円錐（底面の半径4、高さ6）から、切り取られた小さな円錐（底面の半径2、高さ3）の体積を引くことで求めることが出来ます。 したがって、求める体積 V は V = 1 3π× 42 × 6− 1 3π ×22 ×3 = 28π V = 1 3 π × 4 2 × 6 − 1 3 π × 2 2 × 3 = 28 π となります。 ちなみに、今回の問題では、計算に使用する4つの数値をすべて与えましたが、中学3年で学習

超簡単 体積の求め方 苦手な数学を簡単に

2 を途中式を含めて教えてください Clearnote

 まとめ：円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな？？ 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。楕円体の3方向の各半軸 から体積と表面積を計算します。 半軸 a 半軸 b 半軸 c 体積 V 表面積 S お客様の声 アンケート投稿 よくある質問 リンク方法 楕円体の体積 110 /48件 表示件数 1 0424 30歳代 / 会社員楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは（ @t_kun_kamakiri ）。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り

角柱 円柱の表面積と体積の公式 数学fun

Primary算数的体積の求め方ー四角柱ー 筆記 Clearnote

表面積や体積の求め方 (三角柱,四角柱,円柱,球や半球) 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。 この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 （底面の円の面積）＝（半径）×（半径）×（円周率）＝r × r × π= πr 2 （円柱の体積）＝（底面の円の面積）×（高さ）＝πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求める (1) r=5、h立方体や直方体、そして円柱のような立体の体積はすべて、（底面の面積）×（底面を面と垂直方向に平行移動させた距離）を計算することで求まります。 したがって、上図のような斜円柱の体積の求め方も直円柱同様に、 $ V=Sh $ で求めることが出来ます。ここで、高さ h は2つの底面間の距離であることに注意してください。

三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム

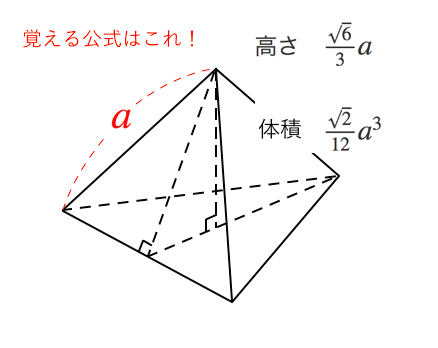
正四面体 高さ 面積を求める公式 苦手な数学を簡単に

 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314 公式の導出方法と計算例については、「円錐の表面積の求め方」をご覧ください。立方体（りっぽうたい）の体積は「1辺の長さの三乗」で計算します。 立方体は辺の長さが全て同じ立体図形です。 1辺が1cmのとき、全ての辺が1cmとなります。 体積の公式は「縦×横×高さ」です。 立方体の全ての辺は同じ長さなので、立方体の体積は「1辺の長さの三乗」です。 今回は立方体の体積の計算、単位、公式、求め方、リットルとの関係について説明し

6年算数 立体の体積 のわかる教え方 いっちに算数 のブログ

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

スマートフォン / 数学公式集 / 体積 ・表面積; もともとの三角柱の高さ＝三角柱の体積÷底面積＝504÷（12×7÷2）＝12（cm） 求める三角柱の高さは、もともとの三角柱の高さの3分の1であることから 求める三角柱の高さ＝12（cm）÷3＝4（cm）となります。 答え 4cm ～立体の体積・表面積を求める公式まとめ〇〇錐という立体の体積は底面積×高さ×\(\frac{ 1 }{ 3 }\)と覚えている方も多いと思いますが、\(\frac{ 1 }{ 3 }\)という係数はここの導出過程から出てくるものです。 球 最後に球の体積についてです。半径\(R\)の球の体積を求めてみたいと思います。

体積の測定 測定のことを 即 知りたい ソクシリ キーエンス

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

 円柱の体積＝7×7×314×12＝（cm³）となります。 答え 円柱ができる。 体積はcm³ ～立体の体積・表面積を求める公式まとめ～ 立方体・直方体の体積の求め方公式 円柱の表面積の求め方公式 三角柱の体積の求め方公式 円錐の体積 三角柱の高さをかけるっ！ さっき計算した「底面積」に「三角柱の高さ」をかけてみよう！ なぜなら、 底面積×高さ を計算すると立体の体積を求めることができるからね。 例題でいうと、 Step1で計算した底面積は10 cm^2、三角柱の高さは10 cmだから、 三角柱ABCDEFの体積は、小学5年生の算数 体積 立体の体積の求め方 練習プリント 小学5年生の算数立体の体積の求め方練習プリントを無料ダウンロード・印刷 （プリント5枚） 小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 小学5年生の算数直方体と立方体を組み合わせ

球の体積と表面積 公式と計算問題と証明 Irohabook

円柱の体積の求め方 公式 小学生 中学生の勉強

の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方底面積と体積の関係、公式は下記が参考になります。 体積の公式は？1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 底面積とは？1分でわかる意味、求め方、円錐、三角錐、四角柱との関係、側面積との違い 100円から読める！ネット不要！印刷しても読みやすいpdf記事は円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S

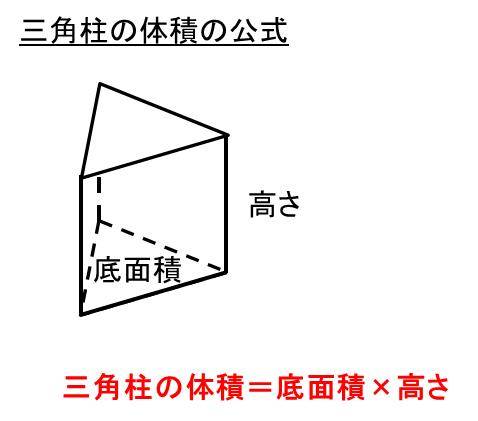
計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく

小5 複雑な立体の体積 直方体 日本語版 Youtube

 立体の体積の求め方（公式）を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方;任意の4つの頂点の座標が与えられた四面体の体積の求め方について解説します． 今までのあらゆる知識を動員して解くので演習効果が高く，個人的には，ベクトルを学ぶ目的の一つにこれを掲げてもいいのではと思っています． 目次 1： 頂点の座標が 立体図形を正しく把握するのが大変です。 回転体の体積の公式も実はこの式で求めているのです。 （切り口が半径f (t)の円なのでS (t)=πf (t) 2 ） 例題：x 2 y 2 ≦1かつy 2 z 2 ≦1を満たす部分の体積を求めよ。 x=tで切るのとz=tで切るのは全く同じであることがわかります。 y=tで切る方法，x=tで切る方法，大学でやる体積の公式を使った方法を示します。 答え

5年 直方体と立方体の体積 算数イメージ動画集 大日本図書

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

６年算数角柱と円柱の体積 立体の体積 教え方

中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット

丸棒の重量 円柱の体積と重量の求め方 鉄の場合

体積の求め方 計算公式一覧

３分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学

球の表面積と体積の公式 数学fun

円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ

複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座

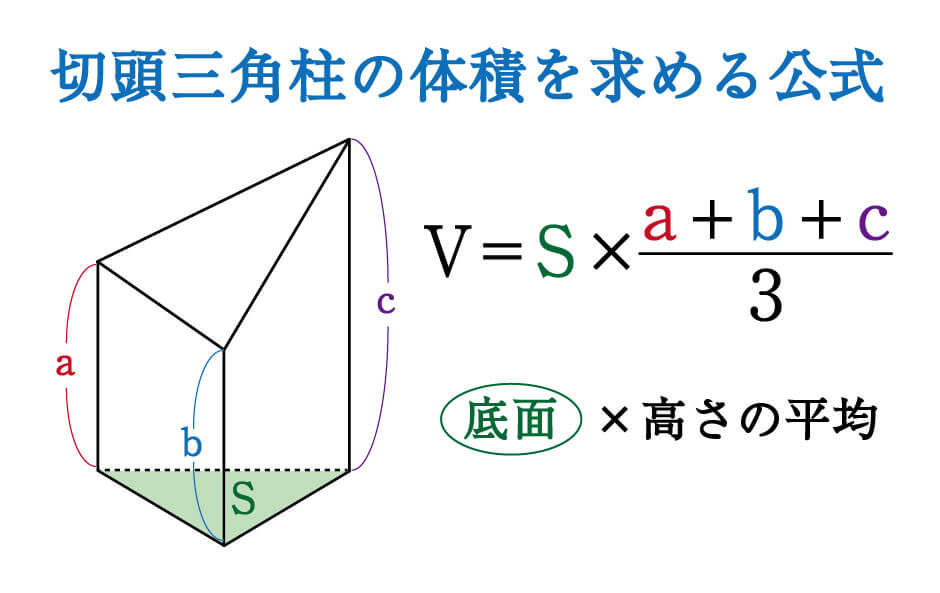
数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ

簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ

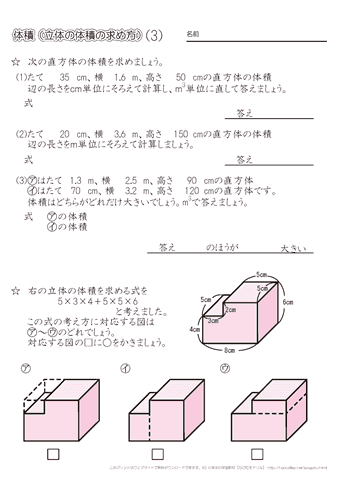
小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

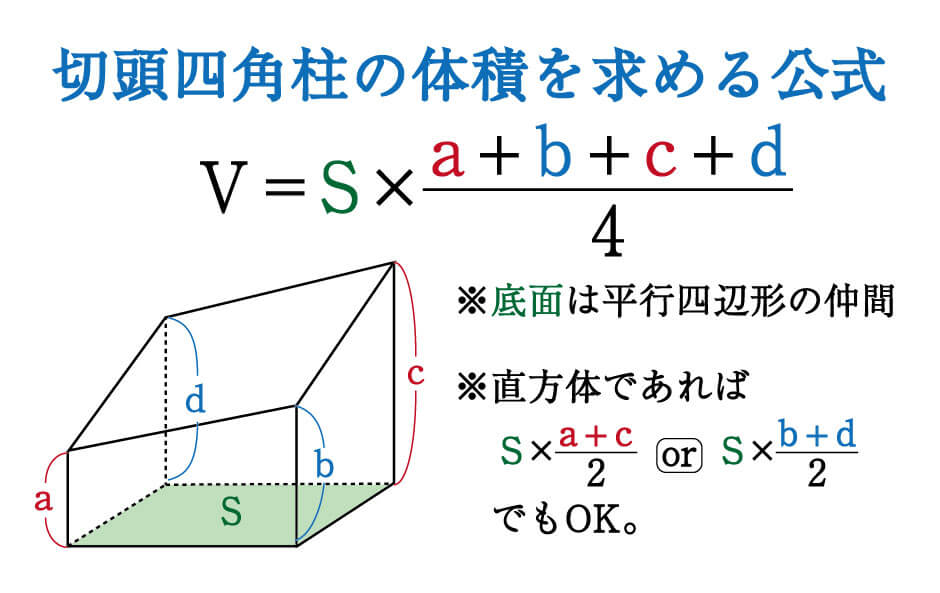
数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋

算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

3分でわかる 円錐の体積 表面積の求め方 合格サプリ

計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

立方体 直方体の体積の求め方 公式 小学生 中学生の勉強

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

立体の体積を求める公式

体積 表面積

中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

体積の求め方 計算公式一覧

1

簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

６年算数角柱と円柱の体積 立体の体積 教え方

容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座

立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun

三角柱の体積の求め方 公式 小学生 中学生の勉強

角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun

立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム

三角柱の体積を求める時にテキストでは2分の1と出ているんですがこれは何なんで Yahoo 知恵袋

体積の求め方 計算公式一覧

計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

中1数学 立体の表面積と体積の求め方と練習問題 Pikuu

角柱と円柱の体積 6年テスト

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

体積の求め方 計算公式一覧

Studydoctor立体の体積の求め方と公式 柱体 中学１年数学 Studydoctor

3

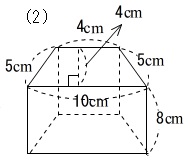
表面積や体積の求め方 三角柱 四角柱 円柱 球や半球

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

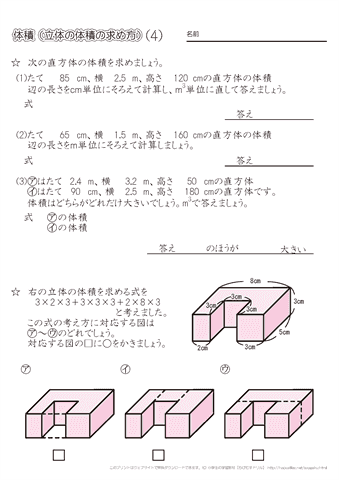
小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 小学校 算数

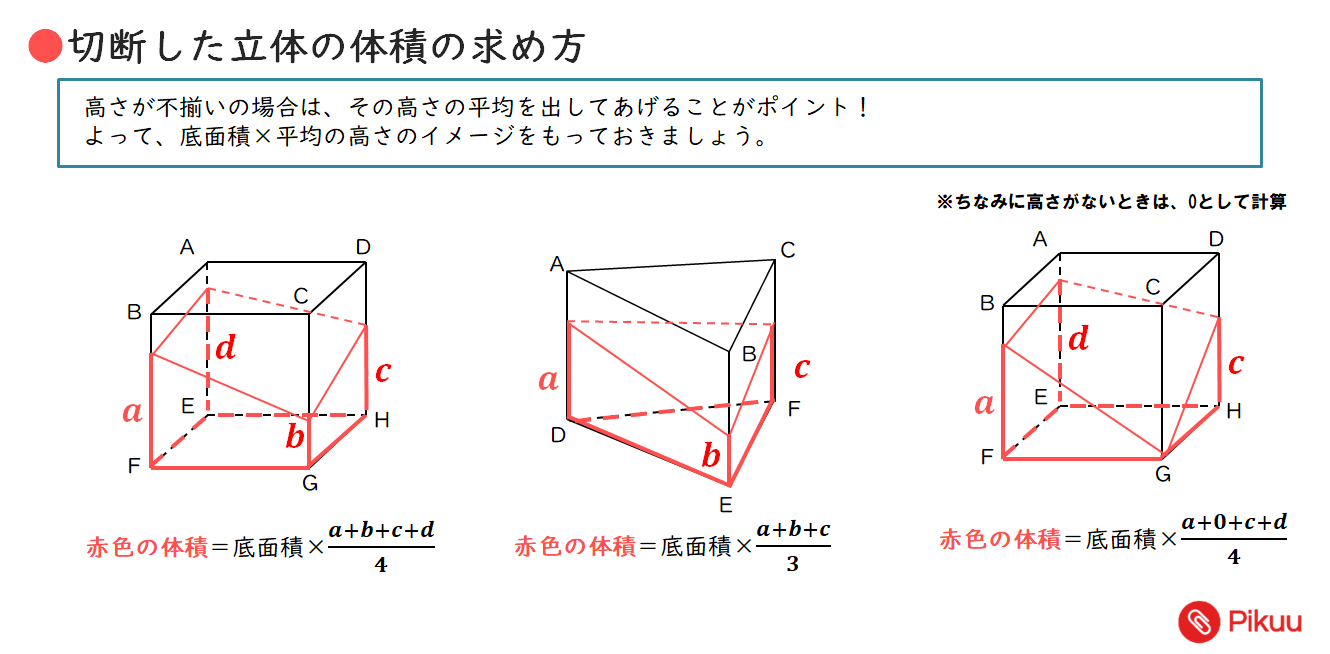
高校入試対策数学 知って得 中学数学の公式テクニック集 Pikuu

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学

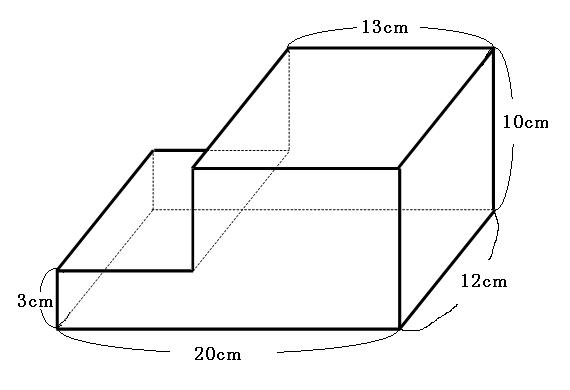
立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー

円柱の表面積と体積を求める公式 具体例で学ぶ数学

中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clearnote

球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典

小５ 算数 小５ ３ 直方体と立方体の体積 Youtube

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

小５ 算数 小５ ５ 体積の求め方のくふう Youtube

体積の求め方 公式一覧 小学生 中学生の勉強

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

角錐 円錐の体積と表面積の公式 数学fun

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト

積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典

私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学

中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clearnote

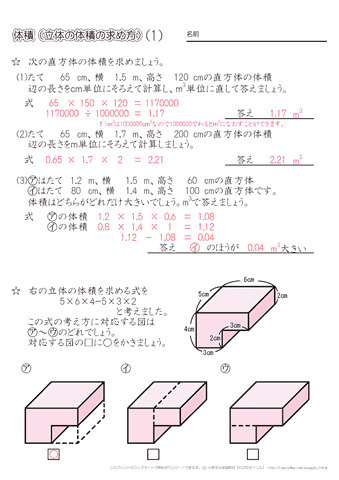
小学５年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生

1

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

体積の公式は 1分でわかる求め方と覚え方 一覧 三角柱 円柱 三角錐の体積

立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun

小学５年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生

三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ

角柱の体積 Youtube

3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ

中1 数学 中1 立体の表面積 Youtube

球の体積の求め方 公式の覚え方を語呂合わせで覚えよう 中学数学 テラコヤプラス By Ameba

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

５年算数体積２わかる教え方

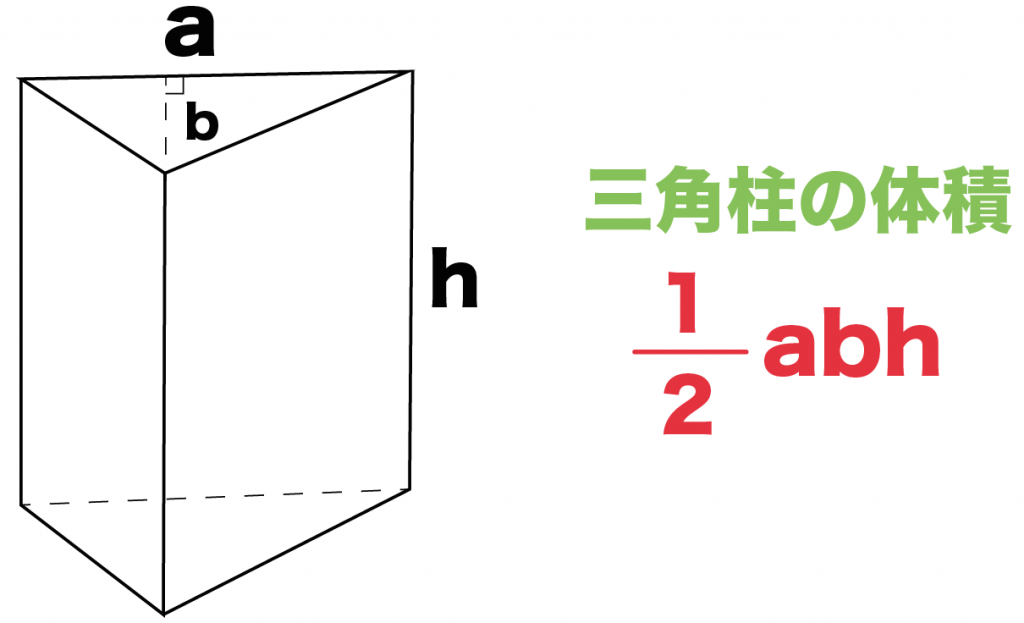
計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく

Incoming Term: 立体の体積の求め方 公式,